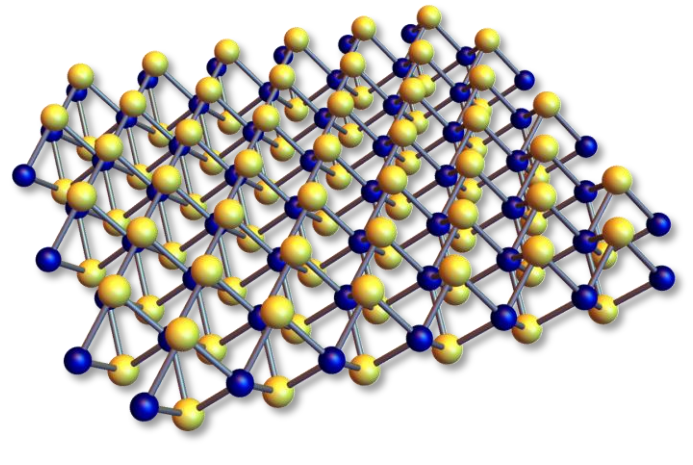
Transition-metal dichalcogenide (TMDC) monolayers
TMDCs are stable, hexagonal (graphene-like, see Fig. 1) semiconductors with a band gap and therefore have a possible wide application in optoelectronics. However, large exciton binding energies have been observed in experiments. The presence of excitons and other charge carrier complexes will greatly influence the optical properties of those materials. In recent experiments, lines ascribed to trions and biexcitons have been observed.
One can consider many different types of charge carrier complexes that can be present in TMDCs (see Fig. 2) varying by the number of electron and holes present in the complex and the relative difference between electron and hole effective masses. E.g. one can consider complexes containing a donor atom, a massive positive charge, that mimics charged impurity in the experiment.
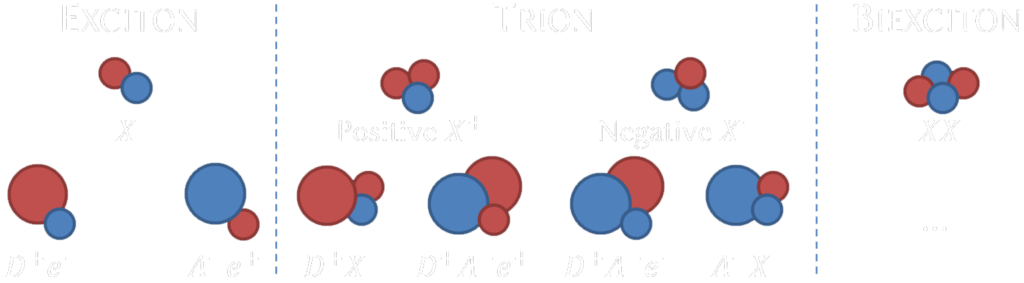
Binding energies of charge carrier complexes
Using the diffusion quantum Monte Carlo approach, we have calculated statistically exact binding energies of various charge carrier complexes using the Mott-Wannier model with Keldysh interaction. We have sampled the full space of parameters, which included the susceptibility of the material $r^*$ and the ratio of effective masses of an electron and a hole.
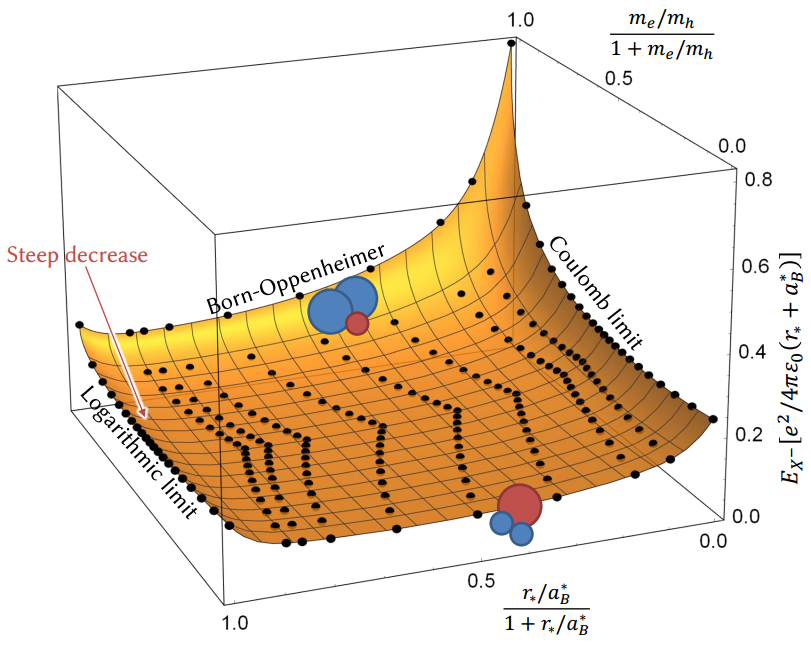
An example result for a negative trion is presented in Fig. 3. We can see that in the light electron limit the negative trion resembles an $H^-$ ion and the energy is linear in the mass ratio. On the other hand, in the heavy electron limit, the trion resembles a $H_2^+$ molecule and one can use the Born-Oppenheimer approximation to prove a square root behaviour of the binding energy in that limit. When the interaction becomes purely logarithmic (the susceptibility is huge) we observe a steep increase in energy compared to the finite values of $r^*$ (susceptibility parameter). Therefore, we conclude that using only the logarithmic interaction may lead to an overestimate in the binding energy, while the DFT results seem to underestimate it.
We have used all our results to produce a high-accuracy fitting curves, which in turn were used to create an easy-to-use, open-access Python program (see Fig. 4).
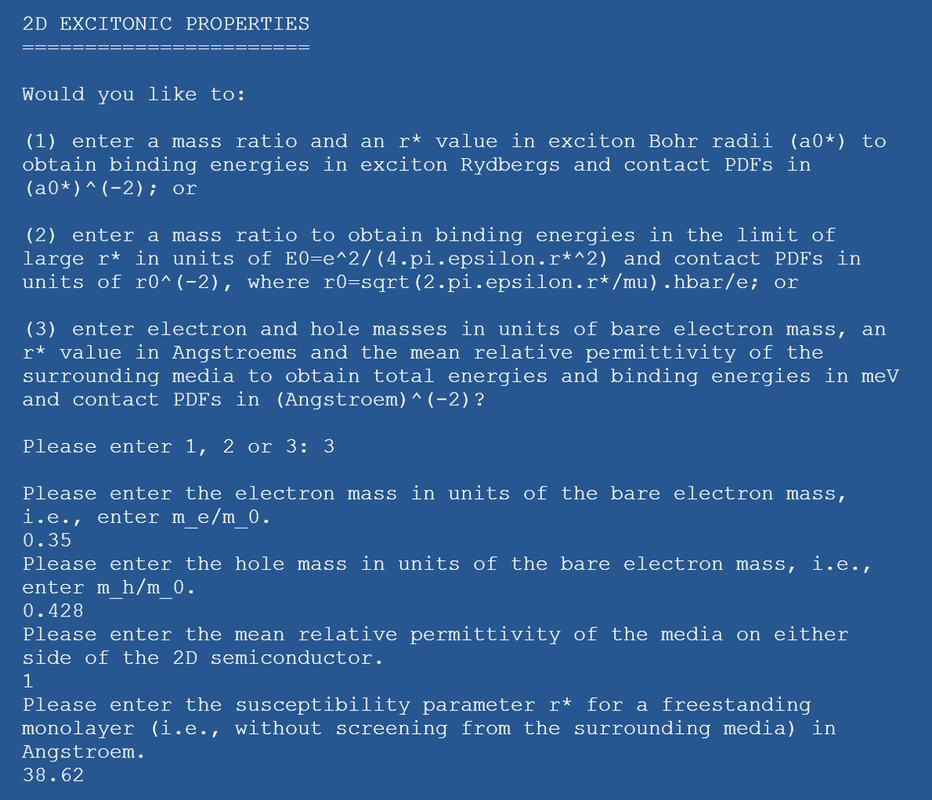
Experimental confirmation
Our results suggest that in the experiment one should see a plethora of peaks corresponding to various complexes. We have theorised that this may have lead to a misclassification of the biexciton peak in previous experiments. A recent article by Barbone et al. has confirmed our expectations. In their article, they show that the peak previously attributed to a biexciton is actually a negative quinton (charged biexction).
Bilayers and multilayers
Introduction of multiple layers in the system modifies the potential energy experienced by the charge carriers even more. Resulting spectrum may be substantially different from the monolayer case: the peaks corresponding to various complexes may be exchanged.