Many-body localisation of zero modes

We wanted to observe if zero modes exhibit interesting properties in the many-body localised phase. To do this, we selected a spin-1 system with chiral symmetry, with the following Hamiltonian:

$$
H = \sum_{i=1}^N S^x_i S^x_{i+1} + \sum_{i=1}^N h_i S^z_i,
$$

where $S^n$ are the spin-1 operators, and the on-site potentials are disordered $h_i\in[-W,W]$.

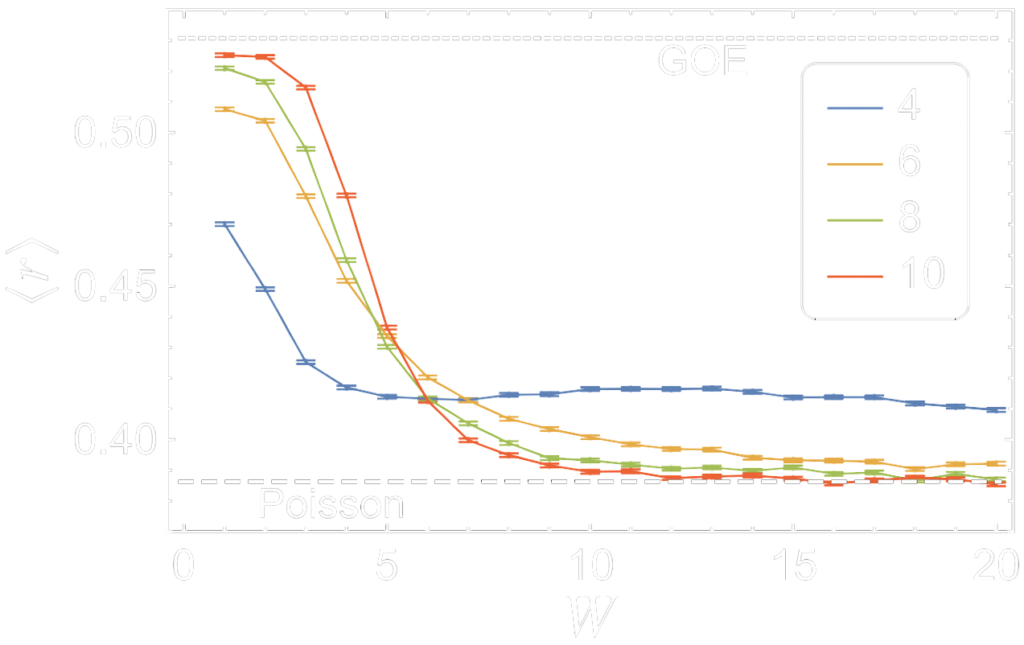
We first determined the transition point between the ergodic and localised regimes, utilising the ratio of the nearby level spacings $\langle r\rangle$ as shown in Fig. 6.

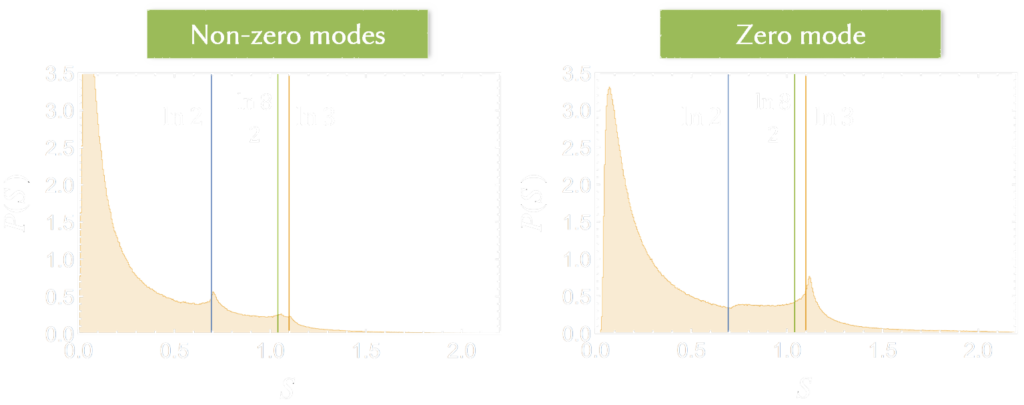
Then, we compared the entanglement entropy histograms between zero modes and non-zero modes in the localised phase (see Fig. 7). This reveals an interesting difference, namely, there are different peaks in both histograms, which correspond to different dimers. Therefore we concluded that many-body localisation causes the production of different dimers between the zero and non-zero modes.