Weak measurements can cause entanglement transition
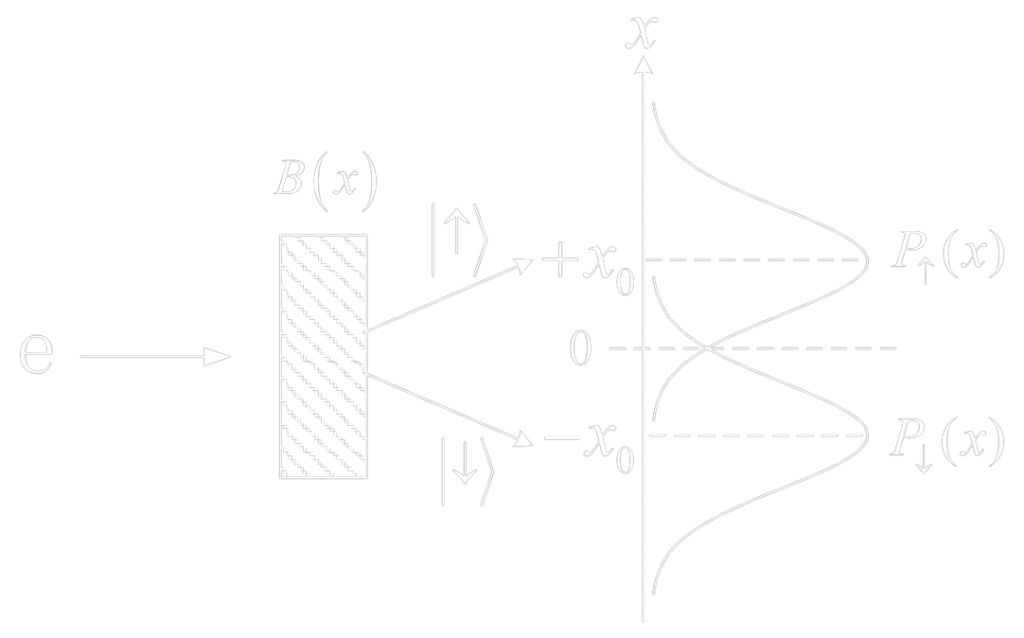
It was recently shown that measurements can be used to cause a quantum Zeno effect: frequent application of measurements can cause localisation in the system. One signature of that is the change from the volume law entanglement behaviour to the area law. In our work, we wanted to see how this situation changes if one uses weak (generalised) measurements: measurements where we have control over how much the system is disturbed by the measuring apparatus (see Fig. 3 for an example implementation).
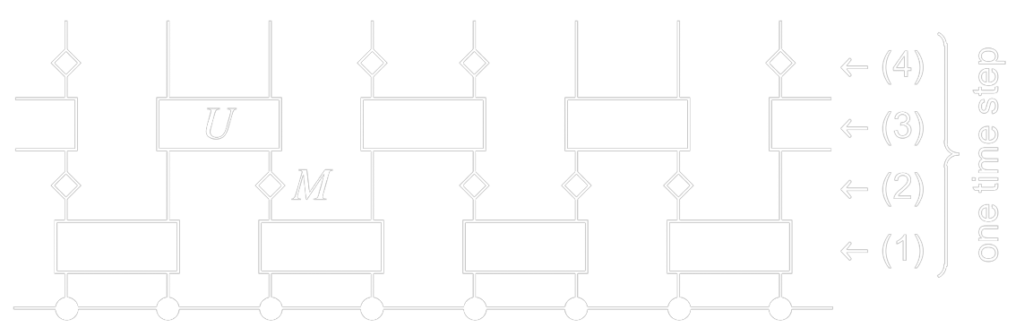
The model consists of a quantum circuit (see Fig. 4), where an initial wavefunction is subjected to the following operations:
- Unitary evolution $U$, which is implemented as random matrices from the Haar measure. This process entangles nearby spins and will favour the volume law.
- Weak measurements $M$ of a certain strength $\lambda/\Delta$ and applied with frequency $p$. Measurements, if strong enough, will break the entanglement and will favour the area law.
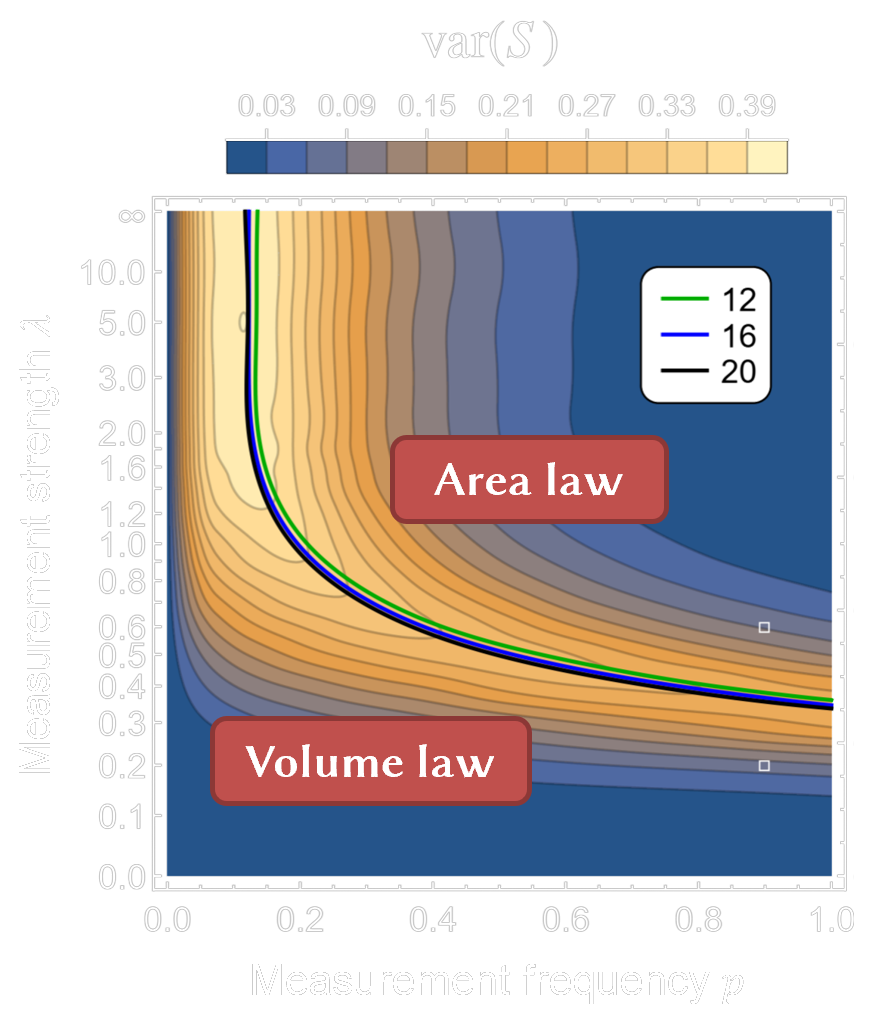
By investigating multiple quantities, namely entanglement entropy $S$, fluctuations of entropy $\text{var}(S)$, and mutual information $I(A:B)$, we have shown that there is a critical value of measurement strength below which there is always a volume law irrespective what the measurement frequency is. There is a similar critical value for the frequency as well.
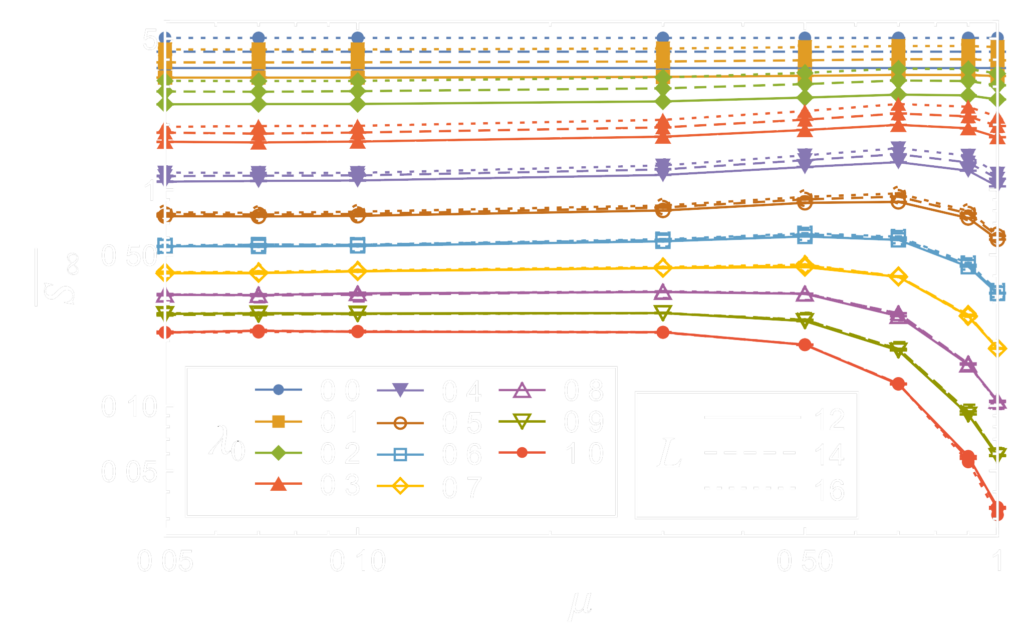
We have also estimated where the transition line lies as a function of measurement strength $\lambda/\Delta$ and measurement frequency, $p$ as shown in Fig. 5.
The universality of the entanglement transition – linking stroboscopic to continuous measurements
Although the transition from the volume law to the area law phase has been thoroughly investigated for the stroboscopic circuit, the corresponding transition for the continuous case was still a matter of debate. In order to address this, we employed two tricks to get to the continuous-time limit:
- We use weak measurements with the measurement strength scaled as $\lambda = \lambda_0 \sqrt{dt}$.
- Instead of completely random unitary matrices from the Haar measure, we use unitary matrices generated by the Poisson kernel with an internal parameter $\mu \sim \sqrt{dt}$. These matrices will range from fully random $(\mu=1)$ to an identity $(\mu=0)$.
When $\mu\to\infty$, we reach the continuous-time limit. Interestingly, one can show that the stroboscopic and the continuous regimes are smoothly connected (see Fig. 8), which suggests that both phase transitions are of the same nature.
1D and 2D Clifford circuits
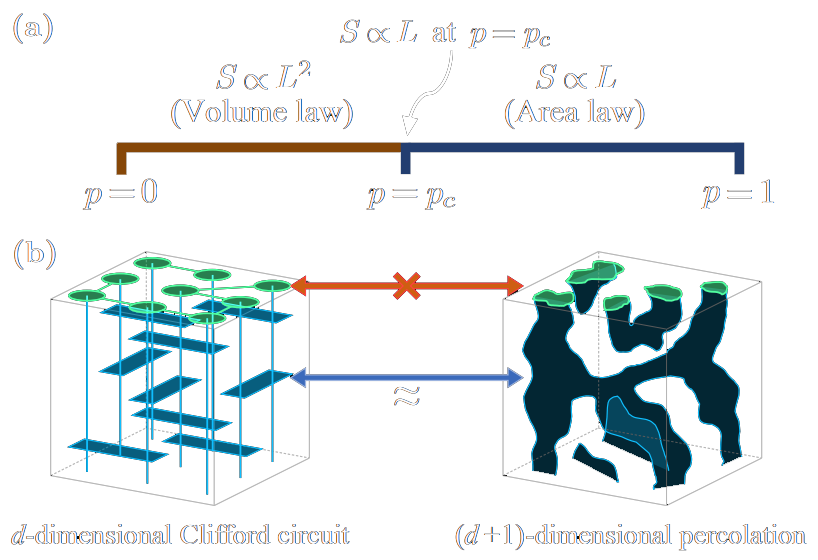
It is known that 1D Clifford circuits undergo a measurement-induced entanglement transition that is in the universality class of the perturbed Potts model. In this research, our aim was to see whether we can see similarities between 1D and 2D Clifford circuits and the universality class of percolation, and whether those similarities break down in the entanglement clusters picture. Clifford circuits can be classicly simulated using many algorithms, but here we have chosen to use the graph representation, which gives direct access to entanglement clusters.
We pinpoint the transition using tripartite mutual information, which is a transition diagnostic showing minimal finite-size effects. Then, we show that:
- At the transition point, entanglement entropy in 2D has an area-law behaviour of $S \sim L$, in agreement with the percolation picture. This is in contrast with the 1D case, where there is a critical logarithmic behaviour of $S \sim \log L$, albeit this is still predicted by percolation.
- All the bulk critical exponents are numerically indistinguishable with percolation.
- However, the surface critical exponents of percolation do not agree with the critical properties of entanglement clusters. This suggests that either the percolation picture breaks down, or that the mapping to percolation is very non-trivial.
Our results have since been corroborated by other research, which directly shows that one can construct a bulk critical exponent that is numerically distinct from percolation. Nonetheless, the percolation picture, albeit approximate, seems to give a good intuitive picture of the entanglement entropy behaviour in monitored Clifford circuits in both 1D and 2D (see Fig. 9).
Monitored free fermions and Anderson localisation
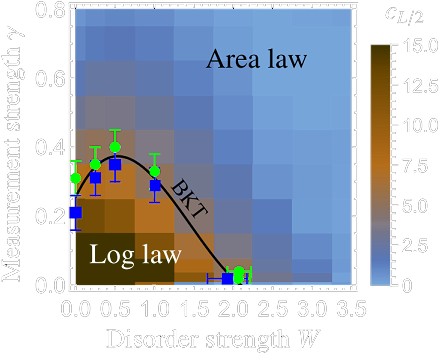
Contrary to interacting models, free fermionic models exhibit a measurement-induced transition in a different universality class: the Berezinskii-Kosterlitz-Thouless transition. Volume law is absent in the phase diagram of monitored free fermions, and instead, the transition happens between the critical phase with logarithmic entanglement and the area law.
In this work, we ask how the disorder impacts this transition. The analysis needs to be done extremely carefully, as the transition is infinite-order and is very hard to capture. We find that the universality class seems to be intact when a random potential is introduced. However, above a certain disorder strength, the critical phase is absent in the diagram. We also find that the introduction of monitoring immediately destroys Anderson localisation.